ಆಳವಿಯ ಆಳ ಬಗೆದ ಆರ್ಕಿಮಿಡೀಸ್
ಕಳೆದ ಬರಹದಲ್ಲಿ ನಾವು ಪಯ್ನ ನೆರವಿನಿಂದ, ಸುತ್ತುಗಳ ಹರವನ್ನು(Area of Circle) ಹೇಗೆ ಸರಾಗವಾಗಿ ಚದರಡಿಗಳಲ್ಲಿ ಲೆಕ್ಕಿಸಬಹುದೆಂದನ್ನು ಅರಿತೆವು. ನೆನಪಿಗಾಗಿ: ಸುತ್ತಿನ ಹರವು = π * (ದುಂಡಿ)2 = π r2. ಈ ಬರಹದಲ್ಲಿ ಗುಂಡುಗಳ ಆಳವಿಯ (Volume) ಒಗಟನ್ನು ಆರ್ಕಿಮಿಡೀಸರು ಹೇಗೆ ಬಿಡಿಸಿದರೆಂದು ತಿಳಿಯೋಣ.
ಆಳವಿಯೆಂದರೆ ಉದ್ದ, ಅಗಲ ಹಾಗೂ ಎತ್ತರ ಹೊಂದಿರುವ ದಟ್ಟಗ (Solid) ತೆಗೆದುಕೊಳ್ಳುವ ಜಾಗ. ಬದಿಗಳುಳ್ಳ (Sides) ದಟ್ಟಗದ ಆಳವಿಯನ್ನು ಅದರ ಉದ್ದ, ಅಗಲ ಹಾಗೂ ಎತ್ತರವನ್ನು ಪೆಚ್ಚಿಸಿ (Multiply) ಎಣಿಸ ಬಿಡಬಹುದು.
ಅಂದರೆ, ಉದ್ದ, ಅಗಲ ಹಾಗೂ ಎತ್ತರ ಎಲ್ಲವೂ ಒಂದೇ ಅಳತೆಯಿರುವ ಮೂರೇರ್ಮಡಿಯ ಆಳವಿಯು (Volume of Cube) = ಉದ್ದ * ಅಗಲ * ಎತ್ತರ. ಮೂರೇರ್ಮಡಿಯ ಉದ್ದ, ಅಗಲ ಹಾಗೂ ಎತ್ತರ ಮೂರು ಮೀಟರ್ ಇದ್ದರೆ ಅದು 27 ಮೀಟರುಗಳ ಮೂರ್ಮಡಿಯಶ್ಟು (Cubic Meter) ಜಾಗ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಉದ್ದ, ಅಗಲ, ಎತ್ತರಗಳು ಬೇರೆ ಬೇರೆಯಿರುವ ಉಬ್ಬುಮೂರೇರ್ಮಡಿಗಳ(Cuboid) ಆಳವಿಯನ್ನೂ ಈ ಪರಿಯಲ್ಲೇ ಲೆಕ್ಕಿಸಬಹುದು. ಕೆಳಗಿನ ತಿಟ್ಟನೋಡಿ,
ಇನ್ನು ಅಡಿಯಿಂದ ಮೇಲಿನವರೆಗೂ ಒಂದೇ ಅಡ್ಡಕೊಯ್ತದ ಹರವುಳ್ಳ (Cross Sectional Area) ದಟ್ಟಗಗಳ ಆಳವಿಯ ಎಣಿಕೆಯೂ ಸರಾಗವೇ. ಅವುಗಳ ಆಳವಿ = ಬುಡದ ಹರವು (Area of Base) * ಎತ್ತರ. ಎತ್ತುಗೆಗೆ ಒಂದು ಉರುಳೆಯನ್ನು (Cylinder) ತೆಗೆದುಕೊಳ್ಳೋಣ.
ಇಲ್ಲಿ ಬುಡವು ಒಂದು ಸುತ್ತಿನಂತಿರುತ್ತದೆ ಹಾಗಾಗಿ, ಆಳವಿ = π r2 * ಎತ್ತರ. ಕೆಳಗಿನ ತಿಟ್ಟದಲ್ಲಿರುವ ಉರುಳೆಯ ಎತ್ತರ = ದುಂಡಿ = 2r ಇದೆ. ಆಳವಿಯು = 8 π r3 ಇರುತ್ತದೆ. [ಮುಂದಿನ ಹಂತದಲ್ಲಿ ಗುಂಡಿನ (sphere )ಆಳವಿಯನ್ನು ಕಂಡುಹಿಡಿಯಲು ಸುಲಬವಾಗಲೆಂದು ಇಲ್ಲಿ ದುಂಡಿ= radius ಗೆ r ಅನ್ನುವ ಬದಲಾಗಿ 2r ಅಂತಾ ಇಟ್ಟುಕೊಳ್ಳಲಾಗಿದೆ]
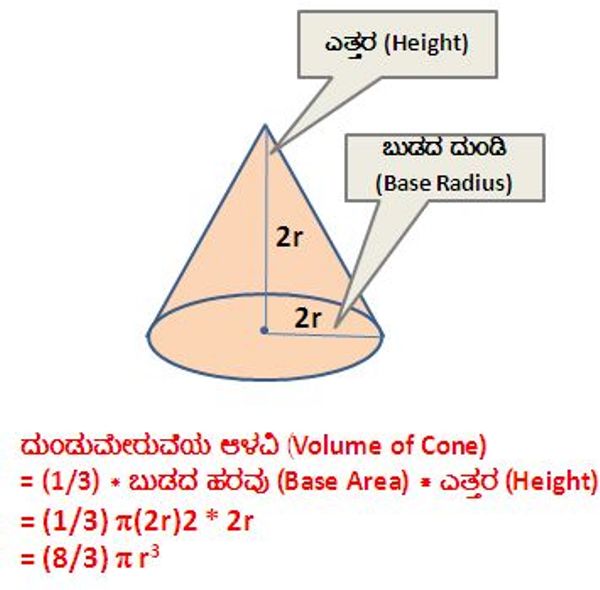
ಇನ್ನು ಅಡಿಯಿಂದ ಮೇಲಿನವರೆಗೂ ಬೇರೆ ಬೇರೆ ಅಡ್ಡಕೊಯ್ತದ ಹರವುಳ್ಳ (Cross Sectional Area) ದಟ್ಟಗಗಳ ಆಳವಿಯ ಎಣಿಕೆಯೂ ಸರಾಗವೇ. ಅವುಗಳ ಆಳವಿ = (1/3) * ಬುಡದ ಹರವು (Area of Base) * ಎತ್ತರ. ಎತ್ತುಗೆಗೆ ಒಂದು ದುಂಡುಮೇರುವೆಯನ್ನು (Cone) ತೆಗೆದುಕೊಳ್ಳೋಣ. ಇಲ್ಲಿ ಬುಡವು ಒಂದು ಸುತ್ತಿನಂತಿರುತ್ತದೆ.
ದುಂಡುಮೇರುವೆಯ ಆಳವಿಯು = (1/3) * π r2 * ಎತ್ತರ. ಕೆಳಗಿನ ತಿಟ್ಟದಲ್ಲಿರುವ ಉರುಳೆಯ ಎತ್ತರ = ಬುಡದ ದುಂಡಿ = 2r ಇದೆ. ಆಳವಿಯು = (8/3) π r3 ಇರುತ್ತದೆ.
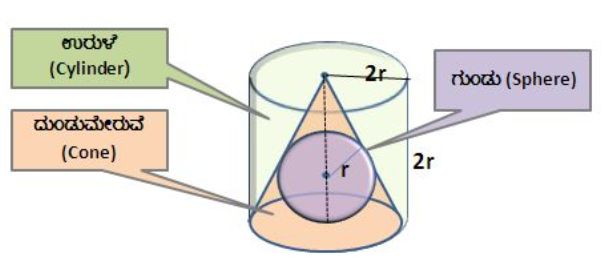
ಇನ್ನು ಮೂರುಕಡೆಯಿಂದಲೂ ದುಂಡಾಗಿರುವ ಗುಂಡುಗಳ (Sphere) ಆಳವಿಯನ್ನು ಹೇಗೆ ಲೆಕ್ಕಿಸುವುದು? ಈ ಒಗಟನ್ನು ಬಿಡಿಸಿದ್ದೂ ನಮ್ಮ ಮೇಲು ಅರಿಗ ಆರ್ಕಿಮಿಡೀಸರೇ. ಹೇಗೆಂದು ಅರಿಯೋಣ ಬನ್ನಿ. ಗುಂಡಿನ ಆಳವಿಯನ್ನು ಬಿಡಿಸಲು ಆರ್ಕಿಮಿಡೀಸರು ತೆಗೆದುಕೊಂಡದ್ದು, ಒಂದು ಉರುಳೆಯಲ್ಲಿ ಕೂರುವಂತಹ ಗುಂಡು ಹಾಗು ದುಂಡುಮೇರುವೆ. ಕೆಳಗಿನ ತಿಟ್ಟವನ್ನು ನೋಡಿ.
ಈ ದಟ್ಟಗಗಳನ್ನು ಮೇಲಿನಿಂದ, ಒಂದೇ ದೂರದಲ್ಲಿ ಅಡ್ಡವಾಗಿ ಕೊಯ್ದರು (ಆ ದೂರವನ್ನು “x” ಅಂದುಕೊಳ್ಳೋಣ). ಹಾಗೆ ಕೊಯ್ದಾಗ ನಮಗೆ ಮೂರು ಬೇರೆ ಬೇರೆ ದುಂಡಿಯಿರುವ ಸುತ್ತುಗಳು ಸಿಗುತ್ತವೆ. ಆ ಸುತ್ತುಗಳಿಗಿರುವ ಹೊಂದಿಕೆಯನ್ನು ಕೆಳಗಿನ ತಿಟ್ಟದಿಂದ ನೋಡೋಣ:
ಉರುಳೆಯ ಅಡ್ಡಕೊಯ್ತದ ಹರವು (Cross Sectional Area of Cylinder)
CACy = 4πr2
ದುಂಡುಮೇರುವೆಯ ಅಡ್ಡಕೊಯ್ತದ ಹರವು (Cross Sectional Area of Cone):
CACo = πx2 — (1)
ಗುಂಡಿನ ಅಡ್ಡಕೊಯ್ತದ ಹರವು (Cross Sectional Area of Sphere):
CASp = π s2 = 2π rx – πx2 –(2)
ಹೊಂದಿಕೆ (1) ಮತ್ತು (2) ಈಗ ಕೂಡೋಣ:
CASp + CACo = 2πrx – πx2 + πx2 = 2πrx
ಎರಡೂ ಬದಿಯನ್ನು 2r ಇಂದ ಗುಣಿಸೋಣ:
2r (CASp + CACo) = 2r (2πrx) = 4πr2x = CACy x
ಇಲ್ಲಿ ಅರಿತಿದ್ದೇನೆಂದರೆ, ಯಾವುದೇ ಮಟ್ಟದಲ್ಲಿ ಇವುಗಳನ್ನು ಅಡ್ಡವಾಗಿ ಕೊಯ್ದರೂ ನಮಗೆ ಸಿಗುವ ಸುತ್ತುಗಳ ಹರವು ಮೇಲಿನ ಹೊಂದಿಕೆಯಲ್ಲೇ ಇರುತ್ತದೆ. ಈಗ ನಾವು ಇವುಗಳನ್ನು ಮೇಲಿನಿಂದ r ಅಶ್ಟು ದೂರದಲ್ಲಿ ಕೊಯ್ದು ಲೆಕ್ಕಿಸೋಣ:
x = r ಆದಾಗ ಕಾಣುವ ಹೊಂದಿಕೆ: 2r (CASp + CACo) = CACy * r
ಆರ್ಕಿಮಿಡೀಸರು ಸನ್ನೆಗೋಲಿನಲ್ಲಿ (Simple Lever) ಕಲಿತಿದ್ದನ್ನು ಇಲ್ಲಿ ಬಳಸಿ ಹೀಗೆ ಹೇಳಿದರು; ಸನ್ನೆಯ ನಡುವಿನಿಂದ ಎಡಕ್ಕೆ 2r ಅಶ್ಟು ದೂರದಲ್ಲಿ ಗುಂಡು ಹಾಗೂ ದುಂಡುಮೇರುವೆ ಇದ್ದು, ಸನ್ನೆಯ ನಡುವಿನ ಬಲಕ್ಕೆ r ದೂರದಲ್ಲಿ ಉರುಳುವೆಯಿದ್ದಾಗ. ಅವುಗಳ ಅಡ್ಡಕೊಯ್ತದ ಹರುವು ಹೊಂದುವಂತಿರುತ್ತದೆ. ಕೆಳಗಿನ ತಿಟ್ಟದಿಂದ ಅದನ್ನು ತೋರಿಸಬಹುದು:
ಮುಂದೆ ಇದೇ ಸನ್ನೆಗೋಲಿನ ಅರಿವನ್ನೇ ಅವುಗಳ ಆಳವಿಗಿರುವ ಹೊಂದಿಕೆ ನೀಡಲು ವಿಸ್ತರಿಸಿದರು. ಕೆಳಗಿನ ತಿಟ್ಟವನ್ನು ನೋಡಿ:
ಒಗಟಿಗೆ ಪರಿಹಾರ ಸಿಕ್ಕೇ ಬಿಟ್ಟಿತು, ಹೇಗೆಂದು ನೋಡಿ:
2r [ ಗೋಳದ ಆಳವಿ (VSp) + ದುಂಡುಮೇರುವೆಯ ಆಳವಿ (VCo) ] = ಉರುಳೆಯ ಆಳವಿ (Vcy) * r
2 ಗೋಳದ ಆಳವಿ (VSp) + 2 ದುಂಡುಮೇರುವೆಯ ಆಳವಿ (VCo) = ಉರುಳೆಯ ಆಳವಿ (Vcy)
2 ಗೋಳದ ಆಳವಿ (VSp) = ಉರುಳೆಯ ಆಳವಿ (Vcy) – 2 ದುಂಡುಮೇರುವೆಯ ಆಳವಿ (VCo)
ಗೋಳದ ಆಳವಿ (VSp) = [ಉರುಳೆಯ ಆಳವಿ (Vcy) /2] – ದುಂಡುಮೇರುವೆಯ ಆಳವಿ (VCo)
ಗೋಳದ ಆಳವಿ (VSp) = (8πr3)/2 – (8πr3/3) [ಈ ಬರಹದ ಮೊದಲು ಇದನ್ನು ಕಲಿತಿದ್ದೆವು ನೋಡಿ]
ಗೋಳದ ಆಳವಿ (VSp) = (4πr3) – (8πr3)/3
ಗೋಳದ ಆಳವಿ (VSp) = 4 πr3/3 ಮೂರ್ಮಡಿಯಳತೆಗಳು
ಈ ಹೊಂದಿಕೆಯನ್ನೇ ಇನ್ನೂ ಕೊಂಚ ಅರಿತಾಗ ನಮಗೆ, ಕಾಣುವ ಇನ್ನೊಂದು ಹೊಂದಿಕೆ:
ಗೋಳದ ಆಳವಿ (VSp) = (2/3) * ಉರುಳೆಯ ಆಳವಿ (Vcy)
ಆ ದಿನಗಳಲ್ಲಿ ದಿಟ್ಟವಾಗಿ ಸಾರಿದ ಈ ಹೊಂದಿಕೆಗಳೇ, ಮುಂದಿನ ದಿನಗಳಲ್ಲಿ ಕಂಡುಹಿಡಿದ ಮಾರ್ಪರಿಮೆ (Calculus) ಅನ್ನು ಬಳಸಿ ನೋಡಿದಾಗಲೂ ಹೊಂದಿಕೆಯೇ ಆಗಿತ್ತು. ಇದರಲ್ಲಿಯೇ ಆರ್ಕಿಮಿಡೀಸರಿಗಿದ್ದ ಜಾಣ್ಮೆಯು ಜಗತ್ತಿಗೇ ಕಂಡಿತ್ತು.
ಮುಂದಿನ ಬರಹದಲ್ಲಿ ಅಲ್ಪನ ಅಹಮಿಕೆಗೆ ಆರಿಹೋದ ಅರಿಮೆಯ ಬೆಳಕು ಇದರಲ್ಲಿ ಈ ಮೇರು ಅರಿಗರ ಕೊನೆಹೇಗಾಯಿತೆಂದು ಅರಿಯೋಣ.










1 Response
[…] ಹಿಂದಿನ ಬರಹದಲ್ಲಿ ಓದಿ ಅರಿತಿದ್ದ ಆರ್ಕಿಮಿಡೀಸ್ರ […]