ಅಳವುಗಳು – ಒಂದು ನೋಟ
400 ಏಡುಗಳ (years) ಹಿಂದೆ ಇಂಗ್ಲೆಂಡಿನಲ್ಲಿ, ಅಯ್ಸಾಕ್ ನ್ಸೂಟನ್ (Isaac Newton) ಇರುವರಿಮೆಯಲ್ಲಿ (Physics) ದೊಡ್ಡಮಟ್ಟದ ಅರಕೆಯನ್ನು ನಡೆಸಿ, ಬಿಣ್ಪು (gravity) ಕುರಿತು ಎಲ್ಲಾ ಮಂದಿಯಲ್ಲೂ ಸೆಲೆಮೂಡುವಹಾಗೆ (interest) ಮಾಡಿದರು. ಸೇಬೊಂದು ಮರದಿಂದ “ಟಂ” ಎಂದು ಅವರ ತಲೆಮೇಲೆ ಬಿದ್ದದ್ದರಿಂದಲೇ ಅವರು ಈ ಅರಕೆಗೆ ಕಡಗುಗೊಂಡರು (inspired) ಎಂಬ ನಂಬಿಕೆಯೂ ಇದೆ. (ಆತ ನಮ್ಮ ಕರಾವಳಿಯವರಾಗಿದ್ದಿದ್ದರೆ, ತಲೆಮೇಲೆ ತೆಂಗಿನಕಾಯಿ ಬಿದ್ದು, ಮುಂದಿನ ಅರಕೆಗೆ ಅವರ ಉಸಿರೇ ಇರುತ್ತಿರಲಿಲ್ಲವೇನೋ!).
ಒಂದು ಸೇಬಿನ ದೆಸೆಯಿಂದ ಈ ಇಳೆಯ ಮಂದಿಗೆಲ್ಲ ಬಿಣ್ಪಿನ/ಒಟ್ಟಲುಸೆಳೆತದ (gravity) ಮುನ್ನೋಟ ದೊರೆತಿದ್ದರೆ, ನಮ್ಮ ಎಂದಿನ ಚಟುವಟಿಕೆಗಳಿಂದ ಈ ಇಡಿಯೆಡೆಯ ಕಾಣದ ಅಳವುಗಳ ಕುರಿತು ನಮಗೆ ಸುಳಿವು ಸಿಗಬಾರದೇಕೆ? ಎತ್ತುಗೆಗಾಗಿ, ಒಂದು ಏರ್ವಣೆಯ (chair) ಮೇಲೆ ನಾವು ಕೂತಾಗ, ನಮ್ಮ ಮಯ್ಯಿ ಆ ಏರ್ವಣೆಯನ್ನು ತೂರಿ ಕೆಳಜಾರುವುದಿಲ್ಲ ಏಕೆ? ನೇಸರನ ಮರೆಹೊತ್ತಿನಲ್ಲಿ (time of eclipse) ಆ ನೇಸರನ ಹಿಂದೆ ಮರೆಯಾದ ಒಂದು ಅರಿಲಿನ (star) ಬೆಳಕು ಕೆಲವೊಮ್ಮೆ ನಮಗೆ ಕಾಣುವುದು ಹೇಗೆ? ಒಂದು ಕಲ್ಲನ್ನು ಒಡೆದು ಪುಡಿಪುಡಿಮಾಡುತ್ತಾ ಹೋದರೆ, ಕೊನೆಯಲ್ಲಿ ನಮಗೆ ಏನು ಸಿಗಬಹುದು?
ಇಂತಹ ನೂರಾರು ಕೇಳ್ವಿಗಳ ಬೆನ್ನತ್ತಿ ಹೋದ ಅರಕೆಗಾರರಿಗೆ, ಈ ಇಡಿಯೆಡೆಯ ಅರಿದಾದ ನಾಲ್ಕು ಅಳವುಗಳು (force) ಕಂಡುಬಂದಿವೆ. ಅವುಗಳ ಕಿರುನೋಟ ಇಲ್ಲಿದೆ.
1. ಒಟ್ಟಲುಸೆಳೆತದ / ಬಿಣ್ಪಿನ ಅಳವು (Gravitational Force): ಮೇಲಕ್ಕೆ ಹಾರಿಸಿದ ಎಲ್ಲವೂ ಮರಳಿ ನೆಲಕ್ಕೆ ಏಕೆ ಅಪ್ಪಳಿಸುತ್ತವೆ ಎಂಬುದರ ಕುರಿತು, ತುಂಬ ಮುಂಚಿನಿಂದಲೂ ಮಂದಿಯಾಳ್ಗಳಲ್ಲಿ ಸೆಲೆಮೂಡಿತ್ತಾದರೂ, ಈ ಕೇಳ್ವಿಯ ಆಳಕ್ಕೆ ಇಳಿದು ಅರಿಸಿದವರು ನ್ಯೂಟನ್ ಹಾಗು ಕಳೆದ ನೂರೇಡಿನ (century) ಅಯನ್ಸ್ಟಾಯ್ನ್ (Einstein). ಇನಿತಾದರೂ ಒಟ್ಟಲು (mass) ಇರುವ ಅಡಕಗಳು (matter) ಒಂದೊಕ್ಕೊಂದು ಸೆಳೆದುಕೊಳ್ಳುತ್ತವೆ. ತಳ್ಳಿಕೊಳ್ಳುವುದಿಲ್ಲ. ಯಾಕೆ ಹೀಗೆ? ಹಾಗೆಯೇ, ಎತ್ತುಬಿಣಿಗೆಯು (lift) ಒಂದೊಮ್ಮೆ ಹಗ್ಗದಿಂದ ಕಡಿದು ನೆಲಕ್ಕೆ ಅಪ್ಪಳಿಸುವಾಗ, ಒಳಗಿದ್ದವನಿಗೆ/ಳಿಗೆ ತೇಲುವ ಒಣರಿಕೆಯಾಗುತ್ತದೆ (feeling). ನೆಲದ ಸೆಳೆತವೇ ಇಲ್ಲವೆಂಬಂತೆ! ಇದ್ಯಾಕೆ?
ಈ ಕೇಳ್ವಿಯ ಬೆನ್ನುಹತ್ತಿ, ಈ ಅಳವಿನ ಗುಟ್ಟು ರಟ್ಟಾಗಿಸಿದವರಲ್ಲಿ ಮೊದಲಿಗ ಅಯನ್ಸ್ಟಾಯ್ನ್. 1905ರಂದು “ಹೊರತಾದ ಹೋಲುಕಟ್ಟಲೆ”ಯನ್ನು (Special Theory of Relativity), 1915ರಂದು “ಹರಡಿದ ಹೋಲುಕಟ್ಟಲೆ”ಯನ್ನು (General Theory of Relativity) ಹೊರತಂದ ಇವರು, ಇಂಬು (space), ಹೊತ್ತು ಹಾಗು ಬಿಣ್ಪನ್ನು ನಾವು ನೋಡುವ ಬಗೆಯನ್ನೇ ಮಾರ್ಪಡಿಸಿಬಿಟ್ಟರು. ಮೇಲ್ಮಯ್ಯಲ್ಲಿ ಈ ಎರಡು ಕಟ್ಟಲೆಗಳು ಹೇಳುವುದು ಇದು.
ಹೊರತಾದ ಹೋಲುಕಟ್ಟಲೆ: ಯಾವ ಅಡಕವೂ ಬೆಳಕಿನ ಉರುಬಿಗಿಂತ (velocity) ಹೆಚ್ಚುಬಿರುಸಿನಿಂದ ಹೋಗಲಾರದು. ಹಾಗೆಯೇ, ಮಾರ್ಪಡದ ಉರುಬಿನಲ್ಲಿ ಸಾಗುತ್ತಿರುವ ಕಟ್ಟುಗಳನ್ನು(frame), ಎಲ್ಲ ಬಗೆಯ ಅಳತೆಗಳಿಗೆ ಗುರುತುಕಟ್ಟುಗಳಾಗಿ (frame of reference) ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ಒಂದು ಗುರುತುಕಟ್ಟಿನಲ್ಲಿ ಅಳೆದ ಹೊತ್ತು, ಉದ್ದ ಇಲ್ಲ ಒಟ್ಟು, ಮತ್ತೊಂದು ಗುರುತುಕಟ್ಟಿನಲ್ಲಿ ಲಾರೆಂಜ್ ಮಾರ್ಪಡಿಕೆಯಂತೆ (Lorentz transformation) ಬದಲಾಗುತ್ತದೆ. ಇದರ ದೊರೆತವೇ ಹೊತ್ತಗಲಿಕೆ (Time Dilation) ಹಾಗು ಉದ್ದಕುಗ್ಗುವಿಕೆ (Length Contraction).
ನನ್ನ ಗುರುತುಕಟ್ಟಿನಲ್ಲಿ ನನ್ನ ಗೆಳೆಯನ ಗುರುತುಕಟ್ಟಿ (ಒಂದು ಬಾನ್ಹಡಗು (Space ship) ಇರಬುಹುದು) ಬೆಳಕಿನ ಹತ್ತಿರದ ಬಿರುಸಿನಲ್ಲಿ ಸಾಗುತ್ತಿದ್ದರೆ, ಅವನ ಹೊತ್ತು ಮಲ್ಲನೆ ಸಾಗಿದಂತೆ ಕಂಡುಬರುತ್ತದೆ. ನನ್ನ 10 ಎವೆಹೊತ್ತು (minute) ಅವನ ಒಂದು ಎವೆಹೊತ್ತಾಗಿರಬಹುದು! ಹೀಗೇ ಸಾಗುತ್ತ ಮುಂದೆ ನಾನು 60ರ ಹರೆಯದವನಾದರೂ, ಆ ಕಡುಬಿರುಸಿನಲ್ಲಿ ಸಾಗುತ್ತಿರುವ ನನ್ನ ಗೆಳೆಯನ ಹರೆಯ ಇನ್ನೂ 30 ಏಡು ದಾಟದಿರಬಹುದು! ಅವನ ಹೊತ್ತಿನ ಈ ಅಗಲಿಕೆಯೇ ಹೊತ್ತಗಲಿಕೆ. ಇನ್ನು, ಅದೇ ಕಡುಬಿರುಸಿನಲ್ಲಿ ಸಾಗುತ್ತಿರುವ ಗುರುತುಕಟ್ಟಿಯೊಳಗಿನ ಎಲ್ಲಾ ಅಡಕಗಳ ಉದ್ದ ಕಿರಿದಾಗುವುದು. ಎತ್ತುಗೆಗಾಗಿ, ಅವನ ಒಂದು ಮೀಟರಿನ ಅಳತೆಗೋಲು ನನಗೆ ಹತ್ತು ಸೆಂಟಿಮೀಟರಿನಂತೆ ಕಾಣಬಹುದು! ಇದೇ ಉದ್ದಕುಗ್ಗುವಿಕೆ. ಬೆರಗಿನ ತಿಳಿವೇನೆಂದರೆ, ಈ ಹೊತ್ತಗಲಿಕೆಯಾಗಲಿ, ಉದ್ದಕುಗ್ಗುವಿಕೆಯಾಗಲಿ ಸಾಗುತ್ತಿರುವ ಗುರುತುಕಟ್ಟಿಯೊಳಿಗಿನ ನನ್ನ ಗೆಳೆಯನಿಗೆ ಅರಿವಾಗುವುದೇ ಇಲ್ಲ! ಅವನಿಗೆಲ್ಲವೂ ನನ್ನಂತೆಯೇ, ಎಲ್ಲರಂತೆಯೇ ಕಾಣಿಸುವುದು. ಈ ಅಗಲ, ಕುಗ್ಗುಗಳ ಆಟ ಬರೀ ನನ್ನ ಕಣ್ಣಿಗಶ್ಟೇ ನಿಲುಕುವ ಬೆರಗು.
ಹರಡಿದ ಹೋಲುಕಟ್ಟಲೆ: ಒಟ್ಟಲು ಇರುವ ಇಡಿಯೆಡೆಯ ಎಲ್ಲಾ ಅಡಕಗಳು, ತನ್ನ ಸುತ್ತಲಿನ ಇಂಬು ಹಾಗು ಹೊತ್ತನ್ನು ಬಗ್ಗಿಸುತ್ತವೆ. ಇಂಬು ಹಾಗು ಹೊತ್ತು ಬೇರೆಬೇರೆಯಂತೆ ನಡೆಯುವ ಆಯಗಳಲ್ಲ. ಒಂದಕ್ಕೊಂದು ಬೆಸೆದು ಬಾಗುವ, ಸೆಟೆಯುವ ಆಯಗಳು. ಒಟ್ಟಲು ಹೆಚ್ಚಿದ್ದಶ್ಟೂ ಬಾಗುವಿಕೆ ಹೆಚ್ಚು. ಈ ಬಾಗಿದ ಇಂಬಿನಲ್ಲಿ ಸಾಗುವ ಒಡಮೆಯ ನೇರಗೆರೆಯೇ (Geodesic) ನಮಗೆ ಆ ಒಟ್ಟಲಿನ ಸೆಳೆತದಂತೆ ಕಾಣುವುದು. ಎತ್ತುಗೆಗಾಗಿ, ನೇಸರಬಳಗವನ್ನೇ (Solar System) ತೆಗೆದುಕೊಳ್ಳೋಣ. ನೇಸರನ ಒಟ್ಟಲು ಹಿರಿದು. ಹಾಗಾಗಿ, ಅದರ ಸುತ್ತಲಿನ ಇಂಬು-ಹೊತ್ತನ್ನು ನೇಸರ ಹಿರಿದಾಗಿಯೇ ಬಾಗಿಸುತ್ತದೆ. ಈ ಬಾಗಿದ ಇಂಬಿನಲ್ಲೇ ಎಲ್ಲಾ ಸುತ್ತುಗಗಳು (Planets) ಸುತ್ತುತ್ತಿರುವುದು.
ಇದರ ಉನ್ನಿಕೆ (imagination) ತೊಡರಿನದ್ದಾದ್ದರಿಂದ, ಎಲ್ಲರಿಗೂ ತಿಳಿಯುವಂತಹ ಇನ್ನೊಂದು ಎತ್ತುಗೆಯನ್ನು ಕೊಡುತ್ತೇನೆ. ಒಂದು ಹಿಗ್ಗುಕವನ್ನು (rubber) ಎಳೆದು, ನಾಲ್ಕು ತುದಿಗಳನ್ನು ಗಟ್ಟಿಯಾಗಿ ಕಟ್ಟಿ, ಅದರಮೇಲೊಂದು ತೂಕದ ಚೆಂಡನ್ನಿಡುತ್ತೀರಿ ಎನ್ನಿ. ಆ ಹಿಗ್ಗುಕ ಚೆಂಡಿನ ತೂಕಕ್ಕೆ ಕೆಳಗೆ ಬಾಗುತ್ತದೆ. ಆಗ, ಆ ಬಾಗಿದ ಎಡೆಯತ್ತ ಚಿಕ್ಕ ಚೆಂಡೊಂದನ್ನು ಅಳವಿನಿಂದ ದೂಡಿರಿ. ಈ ಚೆಂಡು ಉರುಳುತ್ತ ಆ ಬಾಗಿನತ್ತ ಸಾಗುತ್ತದೆ. ಬಾಗಿದ ತಿರುವಿನಲ್ಲೇ ಸಾಗುತ್ತ, ತನ್ನ ಪೊಲವನ್ನು (direction) ಬದಲಿಸುತ್ತದೆ! ಬಾಗಿನಿಂದ ಹೊರಬರುತ್ತಿದ್ದಂತೆ ಮತ್ತೆ ನೇರವಾಗಿ ಸಾಗುತ್ತದೆ. ಆದರೆ ಇಶ್ಟರಲ್ಲಾಗಲೇ ಇದರ ಪೊಲ ಬದಲಾಗಿರುತ್ತದೆ. ಈ ಹಿಗ್ಗುಕದ ಮೇಲಿನಿಂದ ನೋಡಿದವರು, (ಹಿಗ್ಗುಕ ಬಾಗಿರುವುದು ಕಾಣಿಸದಿದ್ದರೆ) ತೂಕದ ಚೆಂಡಿನ ಸೆಳೆತದಿಂದಲೇ ಈ ಚಿಕ್ಕ ಚೆಂಡು ತನ್ನ ಪೊಲವನ್ನು ಬದಲಿಸಿತೆಂದು ತಿಳಿದಾರು!
2. ಮಿನ್ಸೆಳೆತದ ಅಳವು (Electromagnetic Force): ನಾವು ಬಳಸುವ ಹೆಚ್ಚಿನ ಒಡಮೆಗಳಿಗೆ ಮಿಂಚಿನ ಬೇಡಿಕೆ ಇದ್ದೇಯಿದೆ. ಓಡುಲಿಯಿರಬಹುದು (mobiles), ಮಡಿಲೆಣೆಯಿರಬಹುದು (laptops). ಈ ಮಿನ್ಕಸುವಿನ ಹಿನ್ನೆಲೆ ಏನು? ಇದನ್ನು ಅರಸುತ್ತ ಸಾಗಿದವರಲ್ಲಿ ಎದ್ದುಕಾಣುವವರು ಜೇಮ್ಸ್ ಕ್ಲರ್ಕ್ ಮಾಕ್ಸ್ವೆಲ್. 1880ರ ಹೊತ್ತಿನಲ್ಲಿ “ಮಾಕ್ಸ್ವೆಲ್ಸ್ ಲೆಕ್ಕಸಾಟಿಕೆ/ಈಡುಗೆ”ಗಳನ್ನು (Maxwell’s Equations) ಕಂಡುಹಿಡಿದು, ಮಿಂಚು (Electricity) ಹಾಗು ಮುತ್ತುಕದ (Magnetism) ಅಳವನ್ನು ಒಂದುಗೂಡಿಸಿ, ಅವೆರಡೂ ಒಂದೇ ಕಟ್ಟಲೆಯ ಬೇರೆಬೇರೆ ತೋರ್ಪಡಿಕೆಗಳೆಂದು ಸಾರಿದವರು. ಏರಿಳಿತಗಳನ್ನು ಹೊಂದುವ ಮಿನ್ಹರವಿಗೆ (Electric Field) ತಕ್ಕಂತೆ ನೆಟ್ಟಕೋನದಲ್ಲಿ (Right Angle) ಮುತ್ತುಕದ ಹರವೂ ಮೂಡುತ್ತದೆ. ಇವೆರಡರ ಏರಿಳಿತದ ಆಟದ ದೊರೆತವೇ “ಮಿನ್ಸೆಳೆತದ ಸೂಸಿಕೆ” (Electromagnetic Radiation). ನಾವು ಕಾಣುವ ಬೆಳಕು, ತೋರ್ಕದಿರು (X rays), ಕಾಣ್ಕೆಮೀರಿದ ಕದಿರು (Ultraviolet Radiation), ಬಾನ್ಕದಿರು (Gamma Rays), ಬಾನುಲಿಯಲೆ (Radio Waves), ಕಿರು-ಅಲೆ (Micro Waves); ಇವೆಲ್ಲವೂ ಮಿನ್ಸೆಳೆತದ ಸೂಸಿಕೆಯ ಬಳಗದ್ದೇ.
 1930ರ ವರೆಗೆ ಈ ಕಟ್ಟಲೆಯು ಮಿನ್ಸೆಳೆತಕ್ಕೆ ಹೋಲಿಸಿದಂತೆ ಎಲ್ಲವನ್ನೂ ಬಿಡಿಸಿಹೇಳುತ್ತಿತ್ತು. ಆದರೆ, 1920ರ ಹೊತ್ತು ಬಿಡಿಕಟ್ಟಲೆಯು (Quantum Theory) ಹುಟ್ಟಿ, ಬೆಳೆಯುತ್ತಿದ್ದಂತಹ ಹೊತ್ತು. ಬಿಡಿಕಟ್ಟಲೆಯ ನಿಜತನವು ಮನದಟ್ಟಾಗುತ್ತಿದ್ದಂತೆ, ಇರುವರಿಮೆಯ ಉಳಿದೆಲ್ಲ ಕಟ್ಟಲೆಗಳನ್ನು ಇದಕ್ಕೆ ಹೊಂದಿಸುವ ಆರಯ್ಕೆ (Experiment) ನಡೆಯಿತು. ಈ ಆರಯ್ಕೆಯಲ್ಲಿ, ಮಾಕ್ಸ್ವೆಲ್ ಲೆಕ್ಕಸಾಟಿಕೆಗಳನ್ನು ಬಿಡಿಕಟ್ಟಲೆಗೆ ಹೊಂದಿಸುವುದೂ ಒಂದಾಗಿತ್ತು. ಆ ಹೊತ್ತಿಗೆ, ಇರುವರಿಮೆಯಲ್ಲಿ ಅರಿದಾಗಿ ಎರಡು ಕವಲುಗಳಿದ್ದವು. ಮೊದಲನೆಯದು, ಅಯನ್ಸ್ಟಾಯ್ನ ಹೋಲುಕಟ್ಟಲೆ ಹಾಗು ಮಾಕ್ಸ್ವೆಲ್ನ ಲೆಕ್ಕಸಾಟಿಕೆಗಳನ್ನೊಳಗೊಂಡ “ಇಡಿಹರವು ಕಟ್ಟಲೆ” (Classical Field Theory). ಎರಡನೆಯದು, ಆಗಶ್ಟೆ ಹುಟ್ಟಿಕೊಂಡಿದ್ದ “ಬಿಡಿಹರವು ಕಟ್ಟಲೆ” (Quantum Field Theory).
1930ರ ವರೆಗೆ ಈ ಕಟ್ಟಲೆಯು ಮಿನ್ಸೆಳೆತಕ್ಕೆ ಹೋಲಿಸಿದಂತೆ ಎಲ್ಲವನ್ನೂ ಬಿಡಿಸಿಹೇಳುತ್ತಿತ್ತು. ಆದರೆ, 1920ರ ಹೊತ್ತು ಬಿಡಿಕಟ್ಟಲೆಯು (Quantum Theory) ಹುಟ್ಟಿ, ಬೆಳೆಯುತ್ತಿದ್ದಂತಹ ಹೊತ್ತು. ಬಿಡಿಕಟ್ಟಲೆಯ ನಿಜತನವು ಮನದಟ್ಟಾಗುತ್ತಿದ್ದಂತೆ, ಇರುವರಿಮೆಯ ಉಳಿದೆಲ್ಲ ಕಟ್ಟಲೆಗಳನ್ನು ಇದಕ್ಕೆ ಹೊಂದಿಸುವ ಆರಯ್ಕೆ (Experiment) ನಡೆಯಿತು. ಈ ಆರಯ್ಕೆಯಲ್ಲಿ, ಮಾಕ್ಸ್ವೆಲ್ ಲೆಕ್ಕಸಾಟಿಕೆಗಳನ್ನು ಬಿಡಿಕಟ್ಟಲೆಗೆ ಹೊಂದಿಸುವುದೂ ಒಂದಾಗಿತ್ತು. ಆ ಹೊತ್ತಿಗೆ, ಇರುವರಿಮೆಯಲ್ಲಿ ಅರಿದಾಗಿ ಎರಡು ಕವಲುಗಳಿದ್ದವು. ಮೊದಲನೆಯದು, ಅಯನ್ಸ್ಟಾಯ್ನ ಹೋಲುಕಟ್ಟಲೆ ಹಾಗು ಮಾಕ್ಸ್ವೆಲ್ನ ಲೆಕ್ಕಸಾಟಿಕೆಗಳನ್ನೊಳಗೊಂಡ “ಇಡಿಹರವು ಕಟ್ಟಲೆ” (Classical Field Theory). ಎರಡನೆಯದು, ಆಗಶ್ಟೆ ಹುಟ್ಟಿಕೊಂಡಿದ್ದ “ಬಿಡಿಹರವು ಕಟ್ಟಲೆ” (Quantum Field Theory).
ಕಳೆವಣಿ (Electron), ಕೂಡುವಣಿ (Proton), ಬೆಳಕಟ್ಟುಗಳ (Photons) ಹುಗಿಯಾಡುವಿಕೆಯನ್ನು (interaction) ಚೆನ್ನಾಗಿ ವಿವರಿಸಬಲ್ಲ ಬಿಡಿಕಟ್ಟಲೆಯ ನಿಲುಕಿಗೆ “ಇಡಿಹರವಿನ ಕಟ್ಟಲೆ”ಯ ಮಾಕ್ಸ್ವೆಲ್ ಈಡುಗೆಗಳನ್ನು ತರಲು ನಡೆದ ಆರಯ್ಕೆಯ ದೊರೆತವೇ “ಬಿಡಿಮಿಂಚಿನ ಹೊಯ್ದಾಟ” (Quantum Electrodynamics). ಈ ಕಟ್ಟಲೆಯ ತಿರುಳು ಹೀಗಿದೆ: ಮಿನ್ಬೆಲೆಯಿರುವ (Charge) ಎಲ್ಲಾ ಒಡಮೆಗಳು, ನೆನಸಿನ ಬೆಳಕಟ್ಟುಗಳ (Virtual Photons) ಕೊಡುಕೊಳ್ಳುವಿಕೆಯ ಒಡಂಬಡಿಕೆಯಲ್ಲಿ ಯಾವಾಗಲೂ ತೊಡಗಿರುತ್ತವೆ ಹಾಗು ಈ ಒಡಂಬಡಿಕೆಯ ಬಗೆಯು, ಎರಡು ಒಡಮೆಗಳ ನಡುವಿನ ಸೆಳೆತ ಇಲ್ಲ ತಳ್ಳುಗೆಯನ್ನು ತೀರ್ಮಾನಿಸುತ್ತದೆ. ಈ ಅರಿವಿನ ದಾರಿಯಲ್ಲಿ ನೆಗಳಿದವರು (famous) ಜುಲಿಯನ್ ಸ್ವಿಂಗರ್ (Julian Swinger) ಹಾಗು ರಿಚ್ಚಾರ್ಡ್ ಪೆಯ್ನ್ಮೆನ್ (Richard Feynman).
3. ಕಡುನಡುವಿಟ್ಟಳದ ಅಳವು (Strong Nuclear Force): ಯಾವುದೇ ಒಡಮೆಯನ್ನು ತುಂಡರಿಸುತ್ತ ಹೋದಲ್ಲಿ, ಕೊನೆಯದಾಗಿ ತುಂಡರಿಸಲಾಗದ ಒಟ್ಟಲೊಂದು ಸಿಗುತ್ತದೆ ಎಂದು ಹಿಂದಿನ ಅರಕೆಗಾರರು ನಂಬಿದ್ದರು. ಆ ಒಟ್ಟಲೇ ಸೀರ (atom). ಆದರೆ, 20ನೇ ನೂರೇಡಿಯ ಮೊದಲರೆಯ ಆರಯ್ಕೆಗಳು ಈ “ತುಂಡರಿಸಲಾಗದ” ನಂಬಿಕೆಯನ್ನು ಹುಸಿಗೊಳಿಸಿದವು. ಆರಯ್ಯೆಡೆಯಲ್ಲಿ (Laboratory) ಆ ಅರಿಕೆಗಾರರಿಗೆ, ಕಳೆಮಿನ್ಬೆಲೆಯ (negatively charged) ಕಳೆವಣಿಯಲ್ಲದೆ, ಕೂಡುಮಿನ್ಬೆಲೆಯ (positively charged) ಕೂಡುವಣಿಯೂ, ಯಾವ ಮಿನ್ಬೆಲೆಯಿರದ ಇಲ್ಲಹಳಿವುಕವೂ (neutron) ದೊರೆತವು. ಅಲ್ಲಿಂದ ತೆರೆದುಕೊಂಡಿದ್ದೇ, ಸೀರಿನ ಇಟ್ಟಳದ (structure) ಕುರಿತಾದ ಅರಕೆ. ಕೆಲವು ಆರಯ್ಕೆಗಳ ಬಳಿಕ ಕಂಡುಕೊಂಡದ್ದು ಏನೆಂದರೆ, ಕೂಡುವಣಿಗಳು ಹಾಗು ಇಲ್ಲಹಳಿವುಕಗಳು ಒಟ್ಟಿಗೆ ಸೇರಿ, ಸೀರಿನ ನಡುಯೆಡೆಯಲ್ಲಿ ಇರುತ್ತವೆ ಹಾಗು ಈ ಒಟ್ಟಲನ್ನು ಕಳೆವಣಿಗಳು ಸುತ್ತುಬರುತ್ತವೆ. (ಈಗಿನ ಬಿಡಿಕಟ್ಟಲೆಯಂತೆ ಕಳೆವಣಿಗಳು ಸುತ್ತುವುದಿಲ್ಲ, ಬದಲಿಗೆ ನಡುವಿಟ್ಟಳ ಹಾಗು ಕಳೆವಣಿಗಳು ಒಟ್ಟು ಸೇರಿ ಮೂಡಿಸುವ ಬಿಡಿಪಾಡುಗಳಲ್ಲಿ (Quantum States) ಈ ಕಳೆವಣಿಗಳು ಇರುತ್ತವೆ). ಕೂಡುವಣಿಯನ್ನೂ ಇಲ್ಲಹಳಿವುಕವನ್ನೂ ಒಟ್ಟಿಗಿರಿಸುವ ಅಳವೇ ಕಡುನಡುವಿಟ್ಟಳದ ಅಳವು.
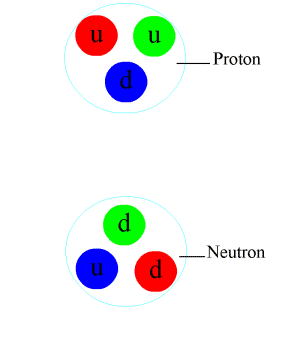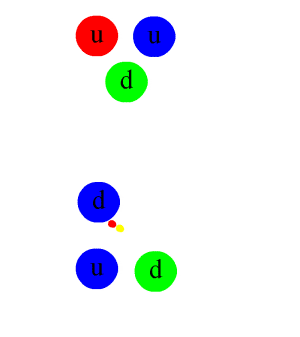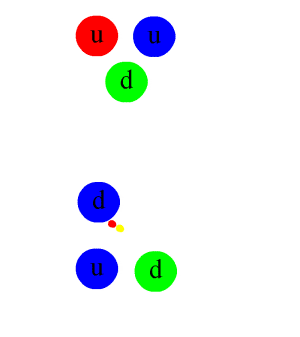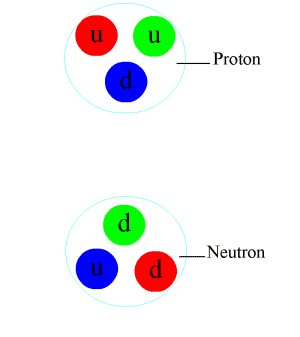 ಈ ಅಳವಿನ ನಡೆಯನ್ನು ವಿವರಿಸುವ ಕಟ್ಟಲೆಯೂ ಬಿಡುಕಟ್ಟಲೆಯಲ್ಲಿ ಒಳಗೊಂಡಿರುವಂತದ್ದು. ಮೇಲಿನ್ಮೇಲೆ ಹೇಳುವುದಾದರೆ, ಕೂಡುವಣಿ ಹಾಗು ಇಲ್ಲಹಳಿವುಕವನ್ನು ಮತ್ತಶ್ಟು ಒಡೆದರೆ, “ಕ್ವಾರ್ಕ್ಸ್ (quarks)” ಎಂಬ ತುಣುಕುಗಳು ಸಿಗುತ್ತವೆ. ಈ ತುಣುಕುಗಳ ಹೆಚ್ಚುಗಾರಿಕೆ ಒರಪು ಸೆರೆ (color confinement) ಎಂಬ ಹುರುಳು (property). ಇದಕ್ಕೆ ತಕ್ಕಂತೆ, ಒಂಟಿಯಾಗಿ ನಮಗೆ ಈ ಕ್ವಾರ್ಕ್ಗಳು ಆರಯ್ಯೆಡೆಯಲ್ಲಿ ದೊರಕುವುದೇ ಇಲ್ಲ. ಯಾವಾಗಲೂ ಎರಡು ಇಲ್ಲ ಹೆಚ್ಚಿನ ತುಣುಕುಗಳು ಒಟ್ಟಿಗೆ ತಗುಲಿಕೊಂಡಿರುತ್ತವೆ. ಎತ್ತುಗೆಗಾಗಿ, ಕೂಡುವಣಿಯಲ್ಲಿ ಎರಡು ಮೇಲ್ತುಣುಕು (up quark) ಹಾಗು ಒಂದು ಕೆಳತುಣುಕು (down quark) ಇದ್ದರೆ, ಇಲ್ಲಹಳಿವುಕದಲ್ಲಿ ಎರಡು ಕೆಳತುಣುಕುಗಳಿದ್ದು ಒಂದೇ ಮೇಲ್ತುಣುಕಿದೆ. (ಕ್ವಾರ್ಕ್ಗಳ ಒರಪುಗಳಲ್ಲಿ ಮೇಲೊರಪು (up color) ಹಾಗು ಕೀಳೊರಪು (down color) ಎಂಬುವೂ ಸೇರಿವೆ).
ಈ ಅಳವಿನ ನಡೆಯನ್ನು ವಿವರಿಸುವ ಕಟ್ಟಲೆಯೂ ಬಿಡುಕಟ್ಟಲೆಯಲ್ಲಿ ಒಳಗೊಂಡಿರುವಂತದ್ದು. ಮೇಲಿನ್ಮೇಲೆ ಹೇಳುವುದಾದರೆ, ಕೂಡುವಣಿ ಹಾಗು ಇಲ್ಲಹಳಿವುಕವನ್ನು ಮತ್ತಶ್ಟು ಒಡೆದರೆ, “ಕ್ವಾರ್ಕ್ಸ್ (quarks)” ಎಂಬ ತುಣುಕುಗಳು ಸಿಗುತ್ತವೆ. ಈ ತುಣುಕುಗಳ ಹೆಚ್ಚುಗಾರಿಕೆ ಒರಪು ಸೆರೆ (color confinement) ಎಂಬ ಹುರುಳು (property). ಇದಕ್ಕೆ ತಕ್ಕಂತೆ, ಒಂಟಿಯಾಗಿ ನಮಗೆ ಈ ಕ್ವಾರ್ಕ್ಗಳು ಆರಯ್ಯೆಡೆಯಲ್ಲಿ ದೊರಕುವುದೇ ಇಲ್ಲ. ಯಾವಾಗಲೂ ಎರಡು ಇಲ್ಲ ಹೆಚ್ಚಿನ ತುಣುಕುಗಳು ಒಟ್ಟಿಗೆ ತಗುಲಿಕೊಂಡಿರುತ್ತವೆ. ಎತ್ತುಗೆಗಾಗಿ, ಕೂಡುವಣಿಯಲ್ಲಿ ಎರಡು ಮೇಲ್ತುಣುಕು (up quark) ಹಾಗು ಒಂದು ಕೆಳತುಣುಕು (down quark) ಇದ್ದರೆ, ಇಲ್ಲಹಳಿವುಕದಲ್ಲಿ ಎರಡು ಕೆಳತುಣುಕುಗಳಿದ್ದು ಒಂದೇ ಮೇಲ್ತುಣುಕಿದೆ. (ಕ್ವಾರ್ಕ್ಗಳ ಒರಪುಗಳಲ್ಲಿ ಮೇಲೊರಪು (up color) ಹಾಗು ಕೀಳೊರಪು (down color) ಎಂಬುವೂ ಸೇರಿವೆ).
ಹಲವು ಬಗೆಯ ಒರಪುಗಳಲ್ಲಿ ಕೂಡಿಕೊಂಡಿರುವ ಈ ತುಣುಕುಗಳು, ತನ್ನ ಒಟ್ಟು ಒರಪನ್ನು ಯಾವಾಗಲೂ ಬಿಳಿಯಾಗಿರಿಸುತ್ತವೆ (ಸೊನ್ನೆಯಾಗಿರಿಸುತ್ತವೆ ಅಂತಲೂ ಹೇಳಬಹುದು. ಇಲ್ಲಿ “ಬಿಳಿ” ಎಂದರೆ, ನಾವು ನೋಡಿ ತಿಳಿದಿರುವ ಬಿಳಿಯೊರಪಲ್ಲ. ಇಲ್ಲಿ ಒರಪು ಎಂದರೆ ನಮ್ಮ ಸುತ್ತಲು ಕಾಣುವ ಒರಪುಗಳೂ ಅಲ್ಲ. ಮಿನ್ಸೆಳೆತಕ್ಕೆ ಮಿನ್ಬೆಲೆಯೆಂಬುದು ಹುರುಳು ಹೇಗೋ ಹಾಗೆಯೇ ನಡುವಿಟ್ಟಳದ ತುಣುಕುಗಳಲ್ಲಿ ಕಂಡುಬರುವ ಹುರುಳು ಒರಪು. ಇದಕ್ಕೆ ಬೇರೆ ಹೆಸರನ್ನೂ ನೀಡಬಹುದು, ತೊಂದರೆಯಿಲ್ಲ!). ಈ ಎಲ್ಲ ತುಣುಕುಗಳನ್ನು ಒಟ್ಟಿಗೆ ಇರಿಸಿಕೊಂಡಿರುವವೇ ಅಂಟುಗಗಳು (gluon). ಮಿನ್ಸೆಳೆತದ ಬೆಳಕಟ್ಟುಗಳಂತೆ ಈ ಅಂಟುಗಳು ತುಣುಕುಗಳ ನಡುವೆ ಹಾರಾಡುತ್ತಿರುತ್ತವೆ ಹಾಗು ಈ ತುಣುಕುಗಳು ಗಟ್ಟಿಯಾಗಿ ಅಂಟಿಕೊಂಡಂತೆ ಇರಲು ನೆರವೀಯುತ್ತವೆ.
4. ಬಡ ನಡುವಿಟ್ಟಳದ ಅಳವು (Weak Nuclear Force): ಮೇಲಿನ ಮೂರು ಅಳವುಗಳು, ಒಡಮೆಗಳನ್ನು ಕೂಡಿಸಿ, ಕಟ್ಟುವ ಕೆಲಸ ಮಾಡುವುದೇ ಹೆಚ್ಚು. ಆದರೆ, ಈ ನಾಲ್ಕನೆಯ ಅಳವು ಒಡಮೆಗಳನ್ನು ಹೆಚ್ಚಾಗಿ ಒಡೆಯುವಂತಹ ಕೆಲಸವನ್ನು ಮಾಡುತ್ತದೆ. ನೀವೆಲ್ಲರೂ ಮೇರಿಕ್ಯೂರಿಯವರ ಹೆಸರನ್ನು ಕೇಳಿರುತ್ತೀರಿ. ಸೀಳ್ಕದಿರು ಸೂಸಿಕೆಯ (Radioactive Radiation) ಕುರಿತು ಅರಿದಾದ ಕೆಲಸವನ್ನು ಮಾಡಿ, ಕೊನೆಗೆ ಆ ಸೂಸುವಿಕೆಯ ಸೊಂಕಿನಿಂದಲೇ ಅಸುತೆತ್ತ (life) ಕಟ್ಟಿಕೆಯರಿಗಳಿವಳು (chemist). ಬಡನಡುವಿಟ್ಟಳದ ಅಳವು, ಈ ಸೀಳ್ಕದಿರು ಸೂಸಿಕೆಯನ್ನು ಬಿಡಿಸಿ ತಿಳಿಸುವುದು. ಇಡಿಯೆಡೆಯ ಎಲ್ಲಾ ಅರೆತಿರುಗಗಳು/ಅರೆತುಂಬಿಣಿತಿರುಗಗಳು (half integer spin = fermions) ಈ ಕಟ್ಟಲೆಗೆ ಒಳಪಟ್ಟಿರುತ್ತವೆ.
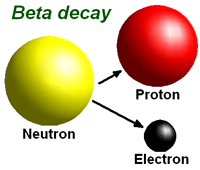
ಇದರಂತೆ, W ಹಾಗು Z ಇಡಿತಿರುಗಗಳ (full integer spins = bosons) ಕೊಡುಕೊಳ್ಳುವಿಕೆಯ ಒಡಂಬಡಿಕೆಯಿಂದಾಗಿ, ಒಂದು ಅರೆತಿರುಗ ಮತ್ತೊಂದು ಅರೆತಿರುಗವಾಗಿ ಮಾರ್ಪಾಡುಗೊಳ್ಳುತ್ತದೆ. ಎತ್ತುಗೆಗಾಗಿ, ಈ ಕಟ್ಟಲೆಯಂತೆ ಇಲ್ಲಹಳಿವುಕವು ಒಡೆದು ಕೂಡುವಣಿ, ಕಳೆವಣಿ ಹಾಗು ಕಡೆ ಕಿರುಇಲ್ಲಹಳಿವುಕವಾಗಿ (anti neutrino) ಮಾರ್ಪಾಡುಗೊಳ್ಳುತ್ತವೆ. ಇದರೊಂದಿಗೆ ಒಂದಿಶ್ಟು ಸೂಸಿಕೆಯೂ ಹರಡುತ್ತದೆ. ಈ ಎಲ್ಲಾ ಒಪ್ಪೆಸಕಕ್ಕೆ (process) ಬೀಟಾ ಸವೆತ (Beta Decay) ಎನ್ನುತ್ತಾರೆ. ಅರಿದಾದ ಮತ್ತೊಂದು ಬಗೆಯ ಸವೆತ, ಆಲ್ಪಾ ಸವೆತ (Alpha Decay).
ಈ ಹೊತ್ತಿಗೆ, ಇಡಿಯೆಡೆಯ ಎಲ್ಲವನ್ನೂ ಈ ನಾಲ್ಕು ಅಳವುಗಳಿಂದ ವಿವರಿಸಬಹುದು. ಈ ಪೊಲದಲ್ಲಿ ಅರಿಗರು ಮುನ್ನುಗ್ಗುತ್ತಿದ್ದಾರೆ. ಅಶ್ಟಲ್ಲದೇ, ಈ ನಾಲಕ್ಕೂ ಅಳವುಗಳನ್ನು ಒಂದೇ ಸೂರಿನಡಿ ತರಲೂ ಹವಣಿಸುತ್ತಿದ್ದಾರೆ. ಇನ್ನೂ ದೊರೆಯದ, ದೊರೆಯುವ ಎಲ್ಲಾ ಬಲ್ಲಮೆಯಿರುವ (possibility) ಆ ಒಂದು ಕಟ್ಟಲೆಯೇ “ಎಲ್ಲವುದರ ಒಕ್ಕಟ್ಟಲೆ” ಇಲ್ಲ “ಇಡಿಕಟ್ಟಲೆ” (Theory of Everything). ಗೆತ್ತ ಇರುವರಿಮೆಯ (Theoretical Physics) ಹೆಚ್ಚಿನ ಎಲ್ಲಾ ಅರಕೆಗಳು ಸಾಗುತ್ತಿರುವುದು ಇದೇ ಪೊಲದಲ್ಲಿ. ಎಲ್ಲವನ್ನೂ ತಿಳಿಯುವ ಹೆಬ್ಬಯಕೆ ಮಂದಿಗನದ್ದು. ಇಡಿಯೆಡೆವೆಣ್ಣು ಈ ಬಯಕೆಗೆ ನೆರವಾಗುತ್ತಾಳೆಯೇ, ತನ್ನ ಮುಗಿಯದ ಸುಳಿಸುಳಿ ಗುಟ್ಟುಗಳಿಂದ ನೀರೆರಚುತ್ತಾಳೆಯೇ, ಕಾದುನೋಡಬೇಕು!
(ತಿಟ್ಟ ಸೆಲೆಗಳು: theconversation.com, 2012books.lardbucket.org, laphysiquemoderne, en.wikipedia.org)






ಇತ್ತೀಚಿನ ಅನಿಸಿಕೆಗಳು