ಲೆಕ್ಕದ ಕಟ್ಟಲೆಗಳು
– ರಗುನಂದನ್.
ಹಿಂದಿನ ಬರಹದಲ್ಲಿ ಬೇರೆ ಬೇರೆ ಬಗೆಯ ಎಣಿಗಳ ಬಗ್ಗೆ ತಿಳಿದುಕೊಂಡಿದ್ದೆವು. ಈ ಬರಹದಲ್ಲಿ ಎಣಿಗಳನ್ನು (numbers) ಬಳಸಿ ಕಟ್ಟಲಾಗಿರುವ ಕೆಲವು ಕಟ್ಟಲೆಗಳ(laws) ಬಗ್ಗೆ ಓದೋಣ.
ಈಗ ತಿಳಿಯಲು ಹೊರಟಿರುವ ಎಣಿಕೆಯರಿಮೆಯ ಟೊಂಗೆಯಲ್ಲಿ (branch of mathematics) ಹೆಚ್ಚಾಗಿ ತುಂಬೆಣಿಗಳನ್ನು (integers) ಬಳಸಲಾಗುತ್ತದೆ. ಸಾಮಾನ್ಯವಾಗಿ ಇದನ್ನು ಅರಿತ್ಮೆಟಿಕ್ (Arithmetic) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಕನ್ನಡದಲ್ಲಿ ಈಗಾಗಲೇ ಲೆಕ್ಕ ಎಂಬ ಪದವನ್ನು ಬಳಸುತ್ತೇವೆ. ಅರಿತ್ಮೆಟಿಕ್ಗೆ ಕನ್ನಡದಲ್ಲಿ ಲೆಕ್ಕ ಇಲ್ಲವೇ ಲೆಕ್ಕದರಿಮೆ ಎನ್ನಬಹುದು.
ಲೆಕ್ಕದರಿಮೆಯು ಕೂಡುವಿಕೆ ಮತ್ತು ಗುಣಿಸುವಿಕೆಯ ಕೆಲವು ಕಟ್ಟಲೆಗಳನ್ನು ನೆಚ್ಚಿದೆ. ಲೆಕ್ಕದಲ್ಲಿ ಅಯ್ದು ಮುಕ್ಯವಾದ ಕಟ್ಟಲೆಗಳಿವೆ –
1. ವರಸೆಯಿರದ ಕೂಡುವಿಕೆಯ ಕಟ್ಟಲೆ (Commutative Law of Addition)
ಈ ಕಟ್ಟಲೆಯ ಪ್ರಕಾರ ಎರಡು ಎಣಿಗಳನ್ನು ಯಾವುದೇ ವರಸೆ (ಓರಣ/order)ಯಲ್ಲಿ ಕೂಡಿದರೂ ಒಟ್ಟು ಮೊತ್ತ(total sum) ಯಾವಾಗಲು ಒಂದೇ ಆಗಿರುತ್ತದೆ.
a+b = b+a
2. ವರಸೆಯಿರದ ಗುಣಿಸುವಿಕೆಯ ಕಟ್ಟಲೆ (Commutative Law of Multiplication)
ಈ ಕಟ್ಟಲೆಯ ಪ್ರಕಾರ ಎರಡು ಎಣಿಗಳನ್ನು ಯಾವುದೇ ವರಸೆ (ಓರಣ/order)ಯಲ್ಲಿ ಗುಣಿಸಿದರೂ ಅವೆರಡರ ಪೆರ್ಚುಗೆಯ ದೊರೆತ (multiplication product) ಯಾವಾಗಲು ಒಂದೇ ಆಗಿರುತ್ತದೆ.
ab = ba
[ನಮಗೆ ತಿಳಿದಿರುವಂತೆ ಕನ್ನಡದಲ್ಲಿ increase ಎಂಬ ಎಸಕಪದಕ್ಕೆ ಹೆಚ್ಚಿಸು ಎಂಬ ಹುರುಳಿದೆ. multiply ಗೆ ಹೆಚ್ಚಿಸು/ಪೆಚ್ಚಿಸು ಎಂಬ ಪದವನ್ನು ಬಳಸಬಹುದು. multiplication ಗೆ ಹಳಗನ್ನಡದ ರೂಪವಾದ ಪೆರ್ಚುಗೆ ಎಂಬ ಪದವನ್ನು ಬಳಸಬಹುದು. Dravidian Etymological Dictionary ಈ ಪದದ ಕುರಿತಾಗಿ ಹೀಗೆ ಹೇಳುತ್ತದೆ:
peccisu to cause to increase, multiply, etc.; percuge, peccuge increase, etc.]
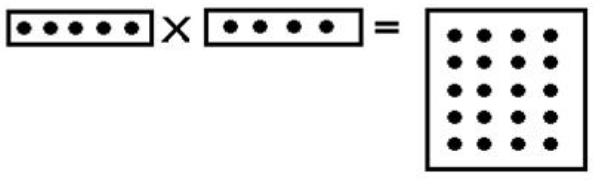
ಕೆಳಗಿನ ತಿಟ್ಟದಲ್ಲಿ ಕಾಣುವಂತೆ 5ಅನ್ನು 4 ಸಲಿ ಹೆಚ್ಚಿಸಲಾಗಿದೆ. ಎರಡು ಎಣಿಗಳನ್ನು ಬಳಸಿ ಹೆಚ್ಚಿಸಿದ ಬಳಿಕ ‘ದೊರೆಯುವ’ multiplication product (4 X 5 = 20) ಅನ್ನು ದೊರೆತ ಎಂದು ಕರೆಯಬಹುದು.
3. ಒಡ ಕೂಡುವಿಕೆಯ ಕಟ್ಟಲೆ (Associative Law of Addition)
ಈ ಕಟ್ಟಲೆಯ ಪ್ರಕಾರ ವರಸೆ ಒಂದೇ ಆಗಿದ್ದಾಗ ಎಣಿಗಳನ್ನು ಬೇರೆ ಬೇರೆ ಗುಂಪುಗಳಾಗಿ ಬಿಡಿಸಿ ಕೂಡಿದರೂ ಒಟ್ಟು ಮೊತ್ತ ಒಂದೇ ಆಗಿರುತ್ತದೆ.
a+(b+c) = (a+b)+c
4. ಒಡ ಗುಣಿಸುವಿಕೆಯ ಕಟ್ಟಲೆ (Associative Law of Multiplication)
ಈ ಕಟ್ಟಲೆಯ ಪ್ರಕಾರ ವರಸೆ ಒಂದೇ ಆಗಿದ್ದಾಗ ಎಣಿಗಳನ್ನು ಬೇರೆ ಬೇರೆ ಗುಂಪುಗಳಾಗಿ ಬಿಡಿಸಿ ಗುಣಿಸಿದರೂ ಪೆರ್ಚುಗೆ (multiplication product) ಒಂದೇ ಆಗಿರುತ್ತದೆ.
a(bc) = (ab)c
5. ಹಂಚಿಕೆಯ ಕಟ್ಟಲೆ (Distributive Law)
ಒಂದು ಮೊತ್ತ(sum; b+c)ವನ್ನು ಎಣಿಯಿಂದ(a) ಗುಣಿಸುವಾಗ ಸಿಗುವ ದೊರೆತವು(product), ಮತ್ತು ಆ ಮೊತ್ತದ ಎರಡು ಬಾಗಗಳನ್ನು ಬೇರೆ ಬೇರೆಯಾಗಿ ಗುಣಿಸಿ, ಬಳಿಕ ಅವೆರಡನ್ನು ಕೂಡಿದರೂ(ab+bc) ಒಟ್ಟು ಮೊತ್ತ ಒಂದೇ ಆಗಿರುತ್ತದೆ.
a(b+c) = ab+ac

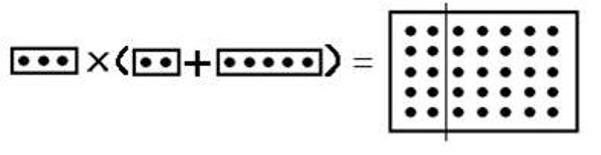




ಇತ್ತೀಚಿನ ಅನಿಸಿಕೆಗಳು