ಮೋಡಿಮಣೆಗಳ ಗುಟ್ಟುಗಳು
– ಬರತ್ ಕುಮಾರ್.
ಇದೊಂದು ಅರಕೆಯ (research) ಬರಹ. ಹಿಂದೊಮ್ಮೆ ಗೆಳೆಯನೊಬ್ಬನ ಮೂಲಕ 3×3 ಮೋಡಿಮಣೆಯ ಬಗ್ಗೆ ತಿಳಿಯಿತು. ಅದರ ಬಗ್ಗೆ ಹೆಚ್ಚು ಅರಕೆ ನಡೆಸಿದಾಗ ಕೆಲವು ಗುಟ್ಟುಗಳು ಕಣ್ಣಿಗೆ ಕಂಡವು. ಅದನ್ನು ಹಂಚಿಕೊಳ್ಳುವುದೇ ಈ ಬರಹದ ಗುರಿ.
ಮೋಡಿಮಣೆ ಎಂದರೇನು?
ಮೋಡಿಮಣೆಯು (Magic square) ಎರಡು ಆಯವಿರುವ ಎಣಿಕೆಯ ಪಟ್ಟಿ. ಇದರಲ್ಲಿ ಬೆಸವೆಣಿಕೆಯ ಮನೆಗಳು ಇರುತ್ತವೆ. ಪ್ರತಿ ಮನೆಯಲ್ಲೂ ಒಂದೊಂದು ಎಣಿಕೆಯನ್ನು ತುಂಬಲಾಗುತ್ತದೆ. ಒಂದು ಮನೆಯಲ್ಲಿರುವ ಎಣಿ ಮತ್ತೊಂದು ಮನೆಯಲ್ಲಿ ಮತ್ತೆ ಬರುವ ಹಾಗಿಲ್ಲ.
ಉದ್ದಸಾಲಾಗಲಿ, ಅಡ್ಡಸಾಲಾಗಲಿ ಇಲ್ಲವೇ ಅರೆಯಡ್ಡ(Diagonal) ಸಾಲಾಗಲಿ, ಆಯ ಸಾಲಿನಲ್ಲಿರುವ ಮನೆಗಳ(cell) ಎಣಿಕೆ ಯಾವಾಗಲು ಬೆಸವೆಣಿಕೆಯೇ(odd number) ಆಗಿರುತ್ತದೆಯಲ್ಲದೆ ಸಾಲಿನಲ್ಲಿರುವ ಎಣಿಗಳನ್ನು ಕೂಡಿದಾಗ, ಸಿಗುವ ಮೊತ್ತವೂ ಒಂದೇ ಆಗಿರುತ್ತದೆ. ಮೊತ್ತವೂ ಕೂಡ ಒಂದು ಬೆಸವೆಣಿಯೇ ಆಗಿರುತ್ತದೆ.
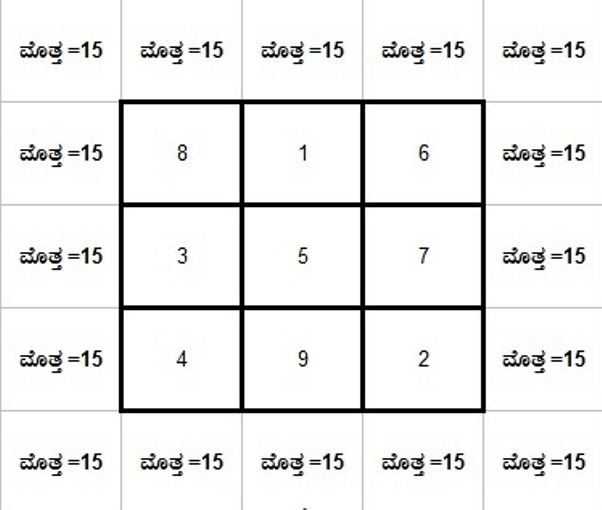
ಎತ್ತುಗೆಗೆ, 3×3 ಮೋಡಿಮಣೆಯ ಸಾಲಿನಲ್ಲಿರುವ ಎಣಿಗಳನ್ನು ಉದ್ದವಾಗಿ/ಅಡ್ಡವಾಗಿ/ಅರೆಯಡ್ದವಾಗಿ ಕೂಡಿದರೆ, ಸಿಗುವ ಮೊತ್ತವು 15 ಆಗಿರುತ್ತದೆ. ಇದರಲ್ಲಿ ಒಟ್ಟು 9 ಮನೆಗಳಿವೆ. ಪ್ರತಿ ಉದ್ದಸಾಲಿನಲ್ಲಿ 3, ಅಡ್ಡಸಾಲಿನಲ್ಲಿ 3, ಅರೆಯಡ್ಡಸಾಲಿನಲ್ಲಿ 3 ಮನೆಗಳಿವೆ.
ನಡುವಿನ ಉದ್ದಸಾಲಿನಲ್ಲೇ ಅಂದರೆ ಎರಡನೇ ಉದ್ದಸಾಲಿನಲ್ಲೇ ಯಾವಾಗಲೂ ಸುರುವಾಗುವ ಎಣಿಕೆ(1) ಮತ್ತು ಕೊನೆಗೊಳ್ಳುವ ಎಣಿಕೆ(9)ಗಳು ಬರುತ್ತವೆ. ಮೋಡಿಮಣೆಯ ಪ್ರತಿಯೊಂದು ಅಂಶವು ಬೆಸವೆಣಿಕೆಗಳ ತುಂಬಿದೆ. ಹಾಗಾಗಿ ಬೆಸವೆಣಿಕೆಗಳ ಮೇಲ್ಮೆಯನ್ನು ಇದರಿಂದ ತಿಳಿದುಕೊಳ್ಳಬಹುದು.
(ತಿಟ್ಟ-1)
ಹಾಗಾದರೆ ಮೋಡಿಮಣೆಯ ಮನೆಗಳಲ್ಲಿ ಎಣಿಗಳನ್ನು ತುಂಬುವುದಾದರೂ ಹೇಗೆ? ಎಂಬ ಕೇಳ್ವಿ ಎದುರಾಗದೇ ಇರದು.
ಮೋಡಿಮಣೆಗೆ ಎಣಿಗಳನ್ನು ತುಂಬುವುದು ಹೇಗೆ?
ಎಣಿಕೆಯರಿಮೆಯಲ್ಲಿ, ಯಾವುದೇ ಬೆಸವೆಣಿಕೆಯನ್ನು 2n+1 ಎಂದು ಗುರುತಿಸಲಾಗುತ್ತದೆ. ಅದರಲ್ಲಿ ’n’ ಎಂಬುದು ತುಂಬೆಣಿಯಾಗಿರಬೇಕು. n=0,1,2,3… ಆದರೆ 2n+1=1,3,5,7… ಆಗಿರುತ್ತದೆ.
- ಯಾವಾಗಲೂ, ನಡುವಲ್ಲಿರುವ ಉದ್ದಸಾಲಿನ ಮೊದಲ ಮನೆಯಿಂದ ಮೋಡಿಮಣೆಯಲ್ಲಿ ತುಂಬುವುದನ್ನು ಶುರು ಮಾಡಬೇಕು ಮತ್ತು ಅದರಲ್ಲಿ ಯಾವಾಗಲೂ ‘1’ ನ್ನು ತುಂಬಬೇಕು.
- ಕೆಳಗಿನ ತಿಟ್ಟದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ 1,2,3…(2n+1)^2 ವರೆಗೆ ಎಣಿಗಳನ್ನು ತುಂಬಬೇಕು. ಅಂದರೆ,
- 3×3 ಮೋಡಿಮಣೆಯಲ್ಲಿ 1 ರಿಂದ 9 ರ ವರೆಗೆ,
- 5×5 ಮೋಡಿಮಣೆಯಲ್ಲಿ 1 ರಿಂದ 25 ರ ವರೆಗೆ,
- 7×7 ಮೋಡಿಮಣೆಯಲ್ಲಿ 1 ರಿಂದ 49 ರ ವರೆಗೆ,
- (2n+1)x(2n+1) ಮೋಡಿಮಣೆಯಲ್ಲಿ 1 ರಿಂದ (2n+1)^2 ರ ವರೆಗೆ ಎಣಿಗಳನ್ನು ತುಂಬಬೇಕು.
(ತಿಟ್ಟ-2)
ಮೋಡಿಮಣೆಯ ಗುಟ್ಟುಗಳು
ಮೋಡಿಮಣೆಯನ್ನು ಚೂಪಾಗಿ ಗವನಿಸಿದರೆ ಅದರಲ್ಲಿ ಕೆಲವು ಗುಟ್ಟುಗಳನ್ನು ಕಾಣಬಹುದು. ಇದನ್ನು ಮರುಪರಿಜು(pattern) ಎಂದೂ ಕರೆಯಬಹುದು. ಕೆಳಗಿನ ತಿಟ್ಟದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ 1 ರಿಂದ 2n+1 ಗಳ ಮೋಡಿಮಣೆಗಳ ಅರೆಯಡ್ಡ ಸಾಲಿನಲ್ಲಿ ಬರುವ ಎಣಿಗಳನ್ನು ಗುರುತಿಸಲಾಗಿದೆ. ಅಲ್ಲದೆ ಅದನ್ನು ಒಂದು ಮೇರುವೆಯ ತರದಲ್ಲಿ ತೋರಲಾಗಿದೆ.
ಹಾಗಾಗಿ (2n+1)x(2n+1) ರ ಮೋಡಿಮಣೆಯನ್ನು ತುಂಬದೇ, ಅದರ ಅರೆಯಡ್ಡಸಾಲಿನಲಿ ಬರುವ ಎಣಿಗಳನ್ನು ಇಲ್ಲಿ ಗುರುತಿಸಬಹುದಾಗಿದೆ ಯಾಕಂದರೆ ಅರೆಯಡ್ಡಸಾಲಿನ ಬಲಮೂಲೆಯಲ್ಲಿ ಬರುವ ಎಣಿ, [(2n+1)2 – (2n+1) x n] ಆಗಿರುತ್ತದೆ. ಇದನ್ನು ತಾಳೆ ನೋಡಲು ನಾವು n=2 ಹಚ್ಚಿ ನೋಡಬಹುದಾಗಿದೆ.
n=2 ಆದರೆ (2n+1) = 5 ಆಗುತ್ತದೆ. ಆಗ ಅರೆಯಡ್ಡ ಸಾಲಿನ ಬಲಮೂಲೆಯಲ್ಲಿ ಬರುವ ಎಣಿ,
= (2×2+1)2 – (2×2+1) x 2
= (4+1)2 – (4+1) x 2
= 52 – 5×2
= 15
ತಿಟ್ಟ 2 ರಿಂದ 15 ಸರಿಯಾಗಿದೆ ಎಂದು ನಿಕ್ಕಿ ಮಾಡಿಕೊಳ್ಳಬಹುದು.
ಅರೆಯಡ್ಡಸಾಲಿನ ಬಲಮೂಲೆಯ ಎಣಿ ದೊರೆತ ಮೇಲೆ ಎಡಮೂಲೆಯ ಎಣಿಯನ್ನು ಹೀಗೆ ಪಡೆಯಬಹುದು,
{[(2n+1)2 – (2n+1) x n]- (2n+1-1) }
= 15 – (5-1)
= 11
{ತಿಟ್ಟ 2 ರಲ್ಲಿ ಇದನ್ನು ತಾಳೆಹಾಕಿ ನಿಕ್ಕಿ ಮಾಡಿಕೊಳ್ಳಬಹುದು}
ಅಂದರೆ, ಬಲಮೂಲೆಯ ಎಣಿಗೂ ಎಡಮೂಲೆಯ ಎಣಿಗೂ ಇರುವ ವ್ಯತ್ಯಾಸ ಯಾವಾಗಲೂ (2n+1-1) ಆಗಿರುತ್ತದೆ.
(ತಿಟ್ಟ-3)
ತೀರಮೆಗಳು:
ಮೇಲೆ ತಿಳಿಸಿದ ಗುಟ್ಟುಗಳಲ್ಲದೆ ಮೋಡಿಮಣೆಗಳಲ್ಲಿ ಇನ್ನೂ ಹಲವು ಗುಟ್ಟುಗಳಿವೆ. ಮೋಡಿಮಣೆಯನ್ನು ಮತ್ತೆ ಮತ್ತೆ ಚೂಪಾಗಿ ಗಮನಿಸಿದರೆ ಗುಟ್ಟುಗಳನ್ನು ರಟ್ಟು ಮಾಡಬಹುದು. ಇವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಕೆಲಸವನ್ನು ಓದುಗರಿಗೆ ಬಿಡಲಾಗಿದೆ.







ಇತ್ತೀಚಿನ ಅನಿಸಿಕೆಗಳು